Hình tam giác đều là một trong những hình học cơ bản và quen thuộc nhất. Tuy nhiên, liệu bạn có biết rằng hình tam giác đều cũng có những đặc điểm thú vị ẩn chứa bên trong? Một trong những điều thú vị đó chính là việc hình tam giác đều có tâm đối xứng hay không.
Trong bài viết này, Học văn vui vẻ sẽ khám phá những bí ẩn xoay quanh câu hỏi “Hình tam giác đều có tâm đối xứng không?”. Từ đó, chúng ta sẽ hiểu rõ hơn về tính chất độc đáo của hình tam giác đều và những ứng dụng thực tế của nó trong cuộc sống.
Định Nghĩa Hình Tam Giác Đều
Trước khi tìm hiểu về tâm đối xứng của hình tam giác đều, chúng ta cần phải hiểu rõ về định nghĩa và đặc điểm của hình tam giác đều.
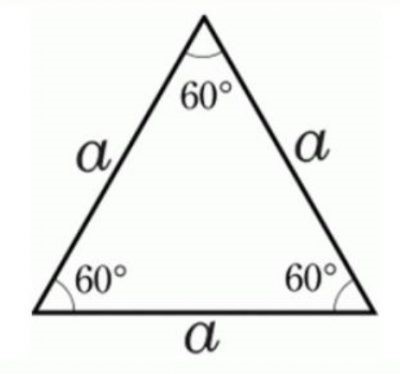
Hình tam giác đều là một hình tam giác có ba cạnh bằng nhau và ba góc bằng nhau, mỗi góc đều bằng 60 độ. Điều này có nghĩa là hình tam giác đều có tính chất đối xứng cao, với các cạnh và góc hoàn toàn giống nhau.
Ngoài ra, hình tam giác đều còn có một số đặc điểm khác như:
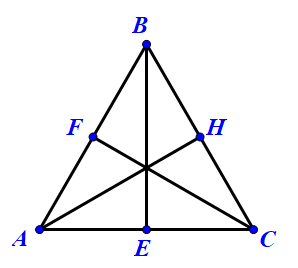
- Có ba trục đối xứng, mỗi trục đều cắt nhau tại một điểm duy nhất – gọi là tâm của hình tam giác.
- Có ba đường cao, ba đường trung trực và ba đường phân giác, tất cả đều cắt nhau tại tâm của hình tam giác.
- Diện tích của hình tam giác đều được tính bằng công thức: S = (√3/4) * a^2, trong đó a là độ dài cạnh của tam giác.
Tâm Đối Xứng Của Hình Tam Giác Đều
Như đã nói ở trên, hình tam giác đều có ba trục đối xứng, mỗi trục đều cắt nhau tại một điểm duy nhất – gọi là tâm của hình tam giác. Vậy tâm của hình tam giác đều có phải là tâm đối xứng không?
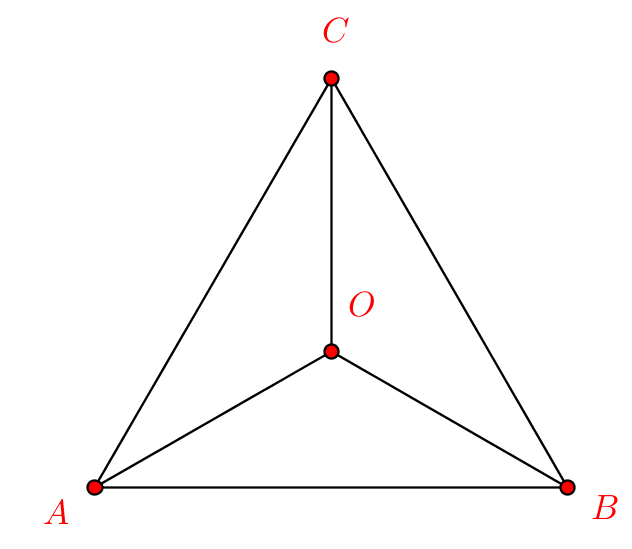
Câu trả lời là CÓ, tâm của hình tam giác đều chính là tâm đối xứng của hình tam giác. Điều này có nghĩa là:
- Mọi điểm nằm trên tam giác đều cách đều so với tâm, tạo thành một hình tròn.
- Bất kỳ đường thẳng nào đi qua tâm của tam giác đều sẽ chia tam giác thành hai phần bằng nhau, tạo thành sự đối xứng.
- Các đường cao, đường trung trực và đường phân giác của tam giác đều đều cắt nhau tại tâm, tạo thành sự đối xứng hoàn hảo.
Như vậy, có thể khẳng định rằng hình tam giác đều chắc chắn có tâm đối xứng. Tâm của hình tam giác đều là điểm giao nhau của ba trục đối xứng, đồng thời cũng là trung điểm của ba cạnh tam giác.
Ứng Dụng Thực Tế Của Tâm Đối Xứng Trong Hình Tam Giác Đều
Tâm đối xứng của hình tam giác đều không chỉ là một tính chất hình học thú vị, mà còn có nhiều ứng dụng thực tế trong cuộc sống. Dưới đây là một số ví dụ:
1. Thiết Kế Kiến Trúc Và Nghệ Thuật
Hình tam giác đều và tâm đối xứng của nó thường được áp dụng trong thiết kế kiến trúc và các tác phẩm nghệ thuật. Ví dụ:
- Trong kiến trúc, nhiều tòa nhà, đền đài, nhà thờ sử dụng hình tam giác đều và tâm đối xứng để tạo ra sự cân bằng, hài hòa và vẻ đẹp thẩm mỹ.
- Trong nghệ thuật, các họa sĩ, điêu khắc gia thường sử dụng hình tam giác đều và tâm đối xứng để tạo ra các tác phẩm mang tính cân đối, đối xứng cao.
- Trong thiết kế nội thất, hình tam giác đều và tâm đối xứng cũng được ứng dụng để tạo ra sự cân bằng và thẩm mỹ cho không gian.
2. Ứng Dụng Trong Kỹ Thuật Và Công Nghệ
Tâm đối xứng của hình tam giác đều cũng có nhiều ứng dụng trong các lĩnh vực kỹ thuật và công nghệ, ví dụ:
- Trong thiết kế anten vô tuyến, hình tam giác đều và tâm đối xứng được sử dụng để tạo ra các anten có hiệu suất cao và phạm vi phủ sóng rộng.
- Trong lĩnh vực quang học, các gương phản xạ và kính lúp cầu có hình dạng tam giác đều và tâm đối xứng để tạo ra các tia sáng song song.
- Trong công nghệ xây dựng, hình tam giác đều và tâm đối xứng được sử dụng để thiết kế các kết cấu bền vững, chịu lực tốt như mái nhà, cầu treo, v.v.
3. Ứng Dụng Trong Thiết Kế Sản Phẩm
Tính chất đối xứng của hình tam giác đều cũng được ứng dụng rộng rãi trong thiết kế các sản phẩm tiêu dùng, ví dụ:
- Trong thiết kế logo và nhận diện thương hiệu, hình tam giác đều và tâm đối xứng thường được sử dụng để tạo ra sự cân đối, ấn tượng và dễ nhận diện.
- Trong thiết kế bao bì sản phẩm, hình tam giác đều và tâm đối xứng giúp tạo ra sự thu hút, tinh tế và dễ nhìn.
- Trong thiết kế nội thất và đồ gia dụng, hình tam giác đều và tâm đối xứng mang lại sự cân bằng, hài hòa và thẩm mỹ cho không gian.
4. Ứng Dụng Trong Toán Học Và Khoa Học

Ngoài các ứng dụng thực tế, tâm đối xứng của hình tam giác đều còn có nhiều ứng dụng trong lĩnh vực toán học và khoa học, ví dụ:
- Trong toán học, tâm đối xứng của tam giác đều được sử dụng để giải các bài toán hình học, tính diện tích, thể tích, v.v.
- Trong vật lý, tam giác đều và tâm đối xứng được ứng dụng trong nghiên cứu về sóng, từ trường, lực học, v.v.
- Trong sinh học, các cấu trúc sinh học như tế bào, hoa, v.v. thường có hình dạng tam giác đều và tâm đối xứng.
Như vậy, tâm đối xứng của hình tam giác đều không chỉ là một tính chất hình học thú vị, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau của cuộc sống. Hiểu rõ về tâm đối xứng của tam giác đều sẽ giúp chúng ta có cái nhìn sâu sắc hơn về thế giới xung quanh.
Kết Luận
Qua bài viết này, chúng ta đã cùng tìm hiểu về tâm đối xứng của hình tam giác đều – một tính chất độc đáo và ẩn chứa nhiều bí ẩn của hình học cơ bản. Từ định nghĩa, đặc điểm đến các ứng dụng thực tế, chúng ta đã khám phá rằng tâm đối xứng của tam giác đều không chỉ là một tính chất hình học, mà còn có nhiều ứng dụng quan trọng trong các lĩnh vực như kiến trúc, nghệ thuật, kỹ thuật, công nghệ, thiết kế sản phẩm và cả toán học, khoa học.
Học văn vui vẻ hy vọng rằng, sau khi đọc bài viết này, bạn sẽ có cái nhìn sâu sắc hơn về hình tam giác đều và tâm đối xứng của nó. Từ đó, bạn có thể áp dụng những kiến thức này vào các lĩnh vực công việc, sở thích hoặc cuộc sống của mình. Chúc bạn khám phá thêm nhiều điều thú vị và ứng dụng hữu ích từ những tính chất đặc biệt của hình học!